¶It's just a state machine

As a simple example, let's say that we have an event, called done, and a bunch of “items”, such as the integers 1, 2, and 3. We want to construct a process that fires the done event exactly once for each item, in any order.

CSP processes can be parameterized, so a good first stab is to keep track of which items are not done yet:

Done(remaining) = done?item : remaining → Done(remaining \ {item})

The remaining parameter gives us the set of items that we haven't fired a done event for. The ‘done?item : remaining’ clause lets the environment choose any of these remaining items, allowing the done event for that item to occur. We then remove that item from the set and repeat. (The ‘?’ handles the base case of this recursion for us; if remaining is empty, then the whole process definition becomes STOP.)

If we plug in a particular value for remaining, we can use the rules from the algebraic semantics to get a simplified definition:

Done({1,2,3}) =
  done.1 → Done({2,3})
    □
  done.2 → Done({1,3})
    □
  done.3 → Done({1,2})

If we repeatedly expand the definitions for every process we encounter, we'll end up with a separate instance of the Done process for each possible subset of ‘{1,2,3}’.

Moreover, we can construct an LTS for these processes. There will be a node for each Done process that we encountered, and an edge for each event that we followed, during the expansion:

An important feature of CSP's operational semantics is that every well-defined CSP process can be described by some LTS. For our refinement algorithm, our question then becomes how to represent these LTS graphs in code.

¶The naïve approach

The simplest answer would be to store the LTS graph directly. You wouldn't even have to write very much code, since you can find a decent pre-canned graph library for just about any programming language you can think of. You'd walk through the operational semantics rules of the process's description, creating explicit nodes and edges in the graph for each subprocess and transition.

This approach has some real advantages. First off, it's conceptually simple: there's a physical graph edge in memory for each transition rule describe by the operational semantics. Second, if you choose a good graph representation, an explicit LTS can be very dense, memory-efficient, and cache-friendly.

However, there is also one very large drawback: CSP processes can get very big, especially once you start using the parallel composition operators. And by "big", I mean "large enough to exhaust your physical memory". This is the "state space explosion" problem that is the bane of any exhaustive formal model checking technique.

Revisiting our example from above, we saw that the LTS for ‘Done({1,2,3})’ had 8 processes in it. The LTS for ‘Done({1,2,3,4})’ is twice as large:

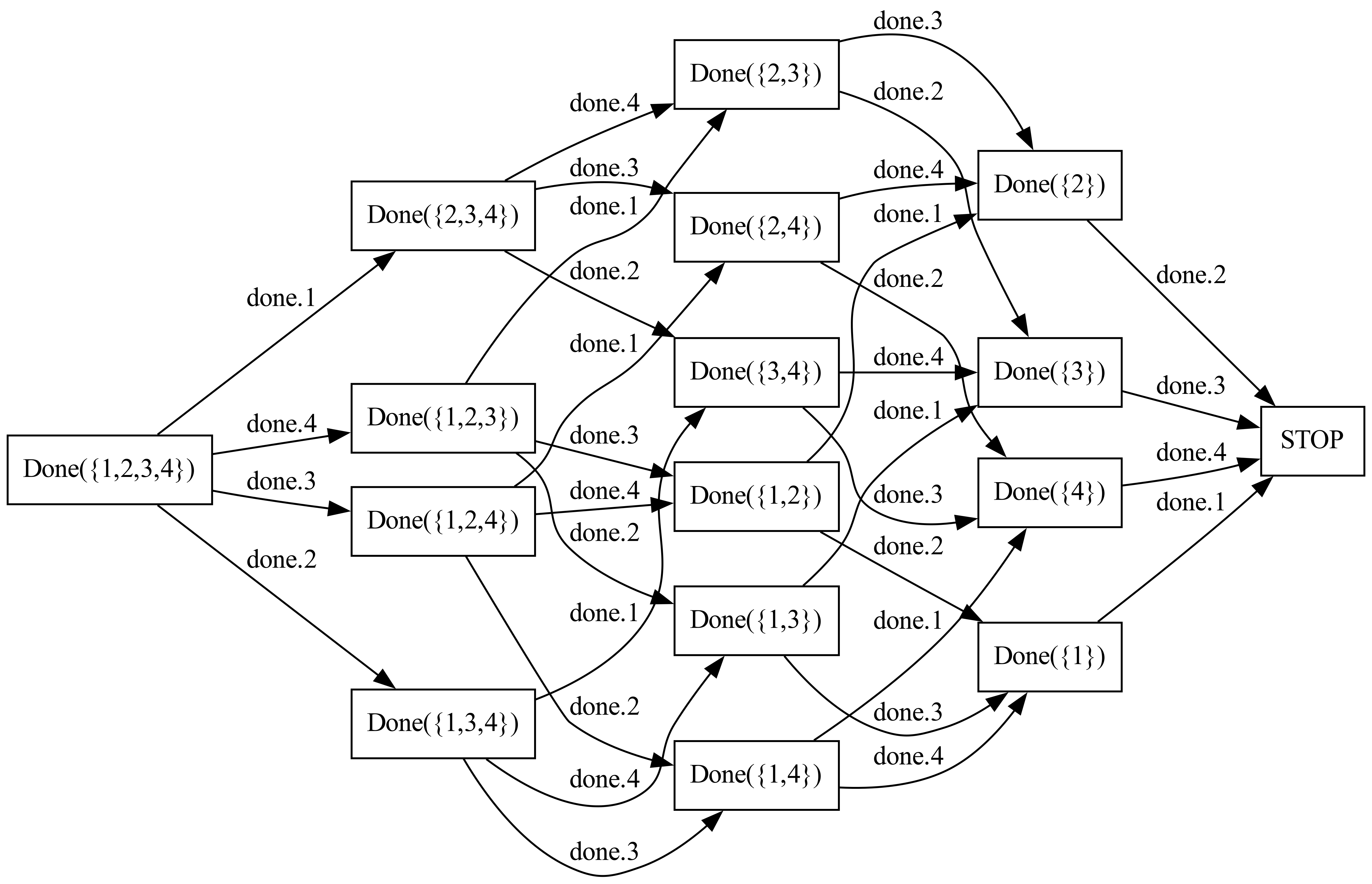
Because of how we've chosen to use a set as our state parameter, the LTS for any Done process is going to have O(2^n) nodes in it, where n is the number of possible elements in the set. This kind of exponential growth is the worst thing you can run across when figuring out how much memory you're going to need! If we need to keep track of 10 items, our LTS is already going to require a thousand distinct nodes. With 20 items, a million nodes. With 30 items, a billion nodes. With 40 items, a trillion nodes. Even if we have a super-efficient graph library at our disposal, which can represent each node in a graph using a single byte of memory, we'd need over a terabyte to represent the LTS for that 40-item Done process.

Tracking 40 items is not an outrageous request, but our process definition gives us something that we can't possibly load into memory at once. We want to avoid creating a full LTS in advance for a large process like this, especially if we don't need to analyze every subprocess to determine whether a particular refinement check holds. This puts us in a bit of a pickle: we want to avoid explicitly creating the full LTS graph of a process, but we still need walk through that LTS graph as part of a refinement check.

¶Laziness to the rescue!

To get around this problem, we need to implement some kind of laziness. Instead of storing the LTS directly, we store a "recipe" for constructing the LTS on the fly, as we need it.

We can implement laziness in a number of different ways. Roscoe spends several pages describing FDR's approach: "supercompilation". Briefly, supercompilation defines an internal language (almost like a bytecode) that can be used to encode the operational semantics rules of each CSP operator.

In HST, we're going to take a different approach. Instead of using something like a bytecode to represent the transition rules, we're going to use code itself, using two common object-oriented patterns: interfaces and visitors. For each CSP operator, we'll implement the following interface:

class Process {
    virtual void initials(std::function<void(Event)> op) const = 0;

    virtual void
    afters(Event initial, std::function<void(const Process&)> op) const = 0;
};

(Did I tell you that I'm implementing HST in C++? Don't run away! I promise it won't be bad!)

This interface tells us for each operator, we need to be able to calculate the process's initials — that is, the set of events that it can perform. And, given one particular initial event, we also need to be able to calculate the afters for that event — that is, the set of processes that you end up in if you follow that event. (If you have any nondeterminism in your process, it's definitely possible for there to multiple processes you might end up in; when the environment chooses this event, it's undefined which of those processes you actually end up in.)

The rules of the operational semantics give us all of the information that we need to implement these two methods for every CSP operator, and all of the other tasks that we need to perform during a refinement check can be implemented in terms of these two methods. And most importantly, we never instantiate a subprocess until it's referenced in some after method. All together, this gives us the right tradeoff between simplicity, flexibility, and control over our memory usage.